Sistemas de Representación
Son conjuntos de convencionalismos que permiten representar en el plano los objetos tridimensionales de modo que sea posible la 'restitución'; esto es, que a partir de la representación bidimensional se puedan conocer las propiedades geométricas de los objetos tales como longitudes, ángulos, etc. En definitiva, son instrumentos que hacen factible el estudio del espacio, que es objetivo propio de la denominada Geometría Descriptiva.
Existen distintas aproximaciones a los Sistemas de Representación que pueden resultar de interés:
- Una clásica, que los considera como fruto de los distintos tipos de proyección: ortogonal, oblicua o central.
- Y otra global, más sencilla -aunque inusual-, que nos permitimos sugerir y recomendar aquí, según la cual una representación no es más que una transformación proyectiva degenerada, y los distintos 'sistemas de representación' son sólo particularidades distintas de esa 'degeneración'.
Aunque, ciertamente, una proyección directa puede ser considerada como una transformación degenerada, lo contrario no necesariamente es cierto; pues, algunas de éstas 'representaciones' podrían ser a lo sumo interpretadas como 'proyecciones de proyección', como se tendrá ocasión de ver. La segunda aproximación resulta, en algún sentido, de mayor generalidad, y permite, incluso, prescindir del concepto de 'proyección'.
Sea como fuere, proyección o transformación, es importante observar que la información perdida con la 'degeneración' debe ser restituida de algún modo; ya con nuevas proyecciones, ya con la expresión -explícita o implícita- de ciertas relaciones entre las entidades representadas. En el modo de solventar el problema estriba precisamente la diferencia entre unos y otros Sistemas de Representación, cada uno de las cuales encuentra su aplicación específica en algún campo de la técnica. Entre ellos están el denominado Sistema Diédrico, el Axonométrico -ortogonal u oblicuo-, el Cónico o el Sistema de Planos Acotados:
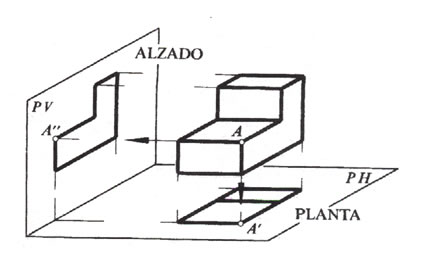
Sistema Diédrico
Se fundamenta en la proyección ortogonal.
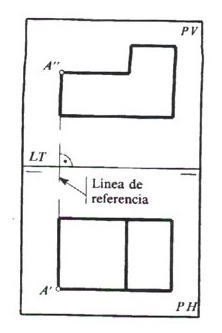
Suple las limitaciones de la proyección única con una segunda proyección también ortogonal sobre un plano ortogonal al primero. Estos planos suelen ser denominados 'horizontal', PH, y 'vertical', PV, siendo las proyecciones o 'vistas' denominadas 'planta' y 'alzado', respectivamente; presentándose estas vistas en un mismo plano tras abatir uno sobre otro alrrededor de la intersección entre ambos, que se denomina 'línea de tierra', LT, y se suele significar con dos tracitos.
|
| ⇒ |

|
El objetivo que persigue es la simplicidad, por lo que el objeto a representar se suele colocar con dos de sus direcciones principales
paralelas a cada plano de proyección. Esto significa que tanto esas dos direcciones como todo lo que esté contenido en planos que las contengan (paralelos al plano de proyección) aparecerá en éste en 'verdadera magnitud'.
En ocasiones, para facilitar la representación o la interpretación del objeto, se emplean nuevas proyecciones, o 'vistas auxiliares',
sobre planos 'siempre ortogonales' a alguna de las anteriores proyecciones.
Aunque el sistema diédrico es el más simple a la hora de representar, tiene el inconveniente de que el intérprete de la representación debe tener la habilidad de integrar en la mente las distintas vistas que se ofrecen para conformar la idea del espacio que se le quiere transmitir. Es, en general, un lenguaje orientado a técnicos, conocedores de dicho lenguaje.
A diferencia de él, otros sistemas, como los que a continuación se muestran, son llamados perspectivas, pues ofrecen una visión global de las tres dimensiones, por lo que pueden ser interpretados por el neófito con más facilidad.
Sistemas Axonométricos
Se fundamentan tanto en la proyección ortogonal como en la oblicua.
Las limitaciones de la proyección única a la hora de 'restituir', o interpretar las tres dimensiones, se suplen implícitamente con las consideraciones de ortogonalidad de las direcciones principales o, explícitamente, añadiendo lineas de referencia paralelas a ellas cuando las direcciones o planos oblicuos en el objeto así lo aconsejen, o incluso, con 'proyecciones de proyección' adicionales si se pretende hacer más explícita la relación del objeto con los planos de proyección.
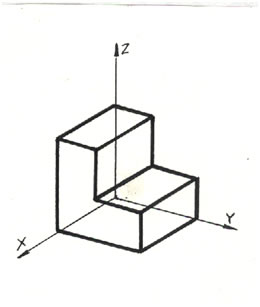
Axonometría ortogonal
Al estar basado en la proyección ortogonal y ser, en general, oblicuas las tres direcciones principales respecto al plano de proyección ninguna de ellas se proyectará en verdadera magnitud, por lo que se requerirán cálculos gráficos adicionales cuando ésta sea necesaria.
|
| ⇒ |
|
A las relaciones entre las longitudes reales en las direcciones principales de referencia, o 'ejes' de sistema, y sus valores en proyección se les llama 'coeficientes de reducción'. Cuando dos de ellas son iguales (por formar sus dos ejes el mismo ángulo con el plano de proyección) al sistema se le denomina 'dimétrico', y si las tres son iguales 'isométrico', resultando en este caso la escala: e = ex = ey = ez = √(2/3) ≈ 0.816;
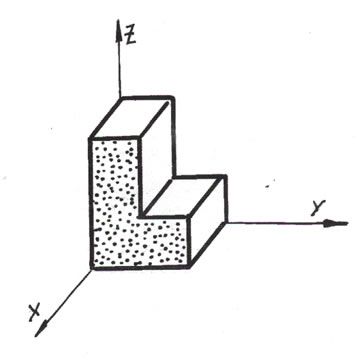
Axonometría oblicua
Para poder proyectar en verdadera magnitud alguno de los planos principales de referencia, sin el inconveniente del sistema diédrico, en el que se pierde completamente la tercera dirección, se hace aquí uso de la proyección oblicua.
La gran ventaja, entonces, de este sistema si se proyecta, como es lo habitual, sobre un plano paralelo a uno de los de referencia es que todo lo paralelo a ese plano aparecerá en verdadera magnitud en la representación, incluidos dos de los tres ejes principales. Esto es, para esos ejes y planos se empleará la escala natural, E1:1, -escala global aparte-, con la comodidad que ello conlleva; pudiendo tomar el tercer coeficiente cualquier valor, si bien, es lo normal adoptar coeficientes de reducción entre 1/2 y 1. Asimismo la interpretación o la medicción directa en el plano pueden resultar más sencillas en algunas ocasiones.
El inconveniente es que el uso de la proyección oblicua trae consigo una cierta deformación, o 'anamorfosis' en la representación que resulta inevitable.
| ⇒ | 
|
A la representación resultante de poner horizontal y vertical los dos ejes en verdadera magnitud se la conoce como 'perspectiva caballera' y cuando el eje oblicuo se coloca vertical 'perspectiva militar', muy empleada en arquitectura.
Sistema Cónico
Se fundamenta en la proyección central.
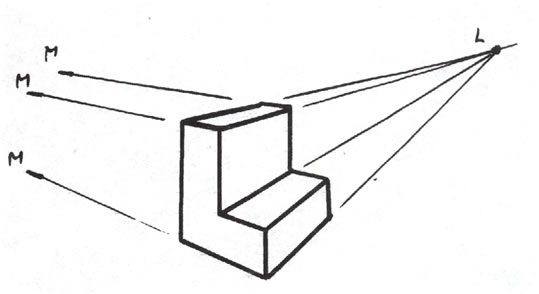
Es notable el hecho de que en este tipo de proyección las rectas paralelas a una determinada dirección no se proyectan como paralelas, como ocurre en las proyecciones cilíndricas -ortogonales u oblicuas-, sino que convergen en un mismo punto, denominado 'punto de fuga' de esa dirección.
|
| ⇒ | 
|
En función de como se coloque el objeto a representar respecto al plano de proyección se puede hablar de sistemas con uno, dos o tres puntos de fuga principales, a los que se les suele denominar perspectiva lineal, cónica y aérea, respectivamente.
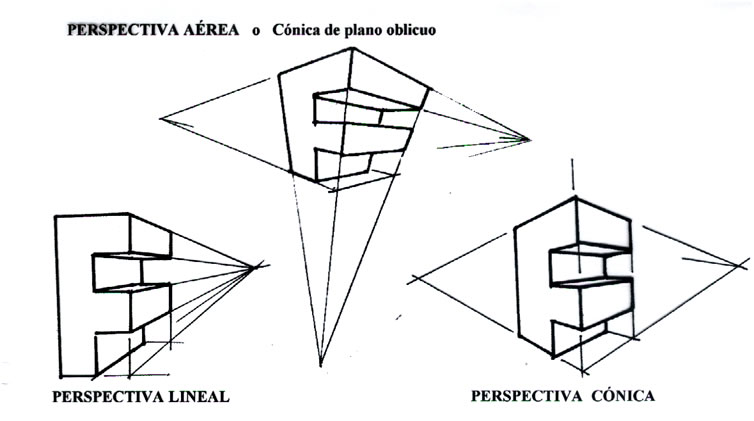
Sistema de Planos Acotados
Se fundamenta en la proyección ortogonal, al igual que el sistema diédrico o la axonometría ortogonal. Pero, resuelve la limitación de la proyección única añadiendo explícitamente indicaciones sobre la tercera dimensión -que no se percibe al proyectar-, esto es, sobre la distancia de cada punto al plano de proyección.
Entre sus aplicaciones más importantes está la representación del terreno, y por extensión de superficies irregulares; en las que la mención de la distancia de cada punto al plano de proyección se suele sustituir por la indicación, en forma de curvas de nivel, de aquellos puntos que están a una determinada distancia del mismo, o 'cotas enteras'.
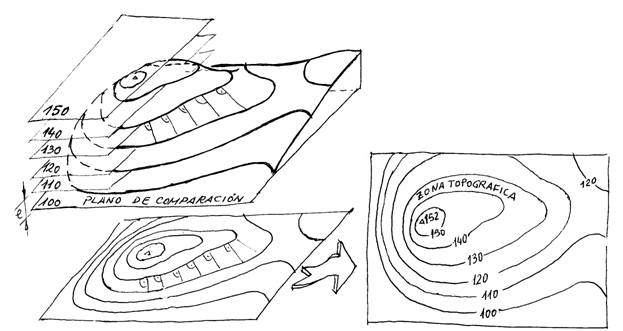
Para un estudio más detallado de cada uno de los sistemas se invita al lector a visitar páginas específicas, como las que puede encontrar en 'wikipedia' u otros sitios especializados:
wikipedia:Proyección gráfica
Y especialmente recomendada, e inusual, es la página "Los Sistemas de Represenrtación como Transformaciones Degeneradas", donde, como se observó anteriormente, se sugiere una visión global de los mismos, según la cual, los distintos sistemas no son más que particularidades distintas de una transformación proyectiva degenerada.
Comentarios y/o sugerencias son bienvenidos en: amadeo@caminos.upm.es.