Los Sistemas de Representación como Transformaciones Degeneradas

Antecedentes:

Sabemos que dadas dos figuras proyectivas, F y F', definir la proyectividad que las hace corresponder equivale a identificar una referencia en una de ellas y su correspondiente en la otra.

Esto significa que cualquier punto Q de F puede ser definido en términos de razones dobles a partir de la referencia en F y, expresando esas mismas razones dobles en la referencia F', puede localizarse Q', homólogo de Q.

En el espacio, 3D, identificar una referencia proyectiva respecto a la cual poder expresar la posición de cualquier punto Q en términos de razones dobles, equivale a identificar cinco puntos (en general, n+2 puntos siendo n la dimensión del espacio) tales que no haya tres alineados.

Esto es, conocer cinco puntos en una figura {OUVWP} y sus correspondientes en la otra {O'U'V'W'P'} equivale a tener definida la proyectividad única que relaciona F con F', y poder obtener el homólogo Q' de cualquier Q dado. En la figura se sugiere la posibilidad de obtener Q' como intersección de r' y s', por elegir una entre otras muchas formas, todas ellas basadas siempre y exclusivamente en la conservación de la razón doble.

De modo equivalente, pero de especial interés como se verá, puede optarse por definir una referencia proyectiva tridimensional como terna de referencias proyectivas unidimensionales de origen común, {OUVWLMN}, pues determinar el quinto punto P de la referencia {OUVWP}, dando por ejemplo sus tres coordenadas respecto a OUVW, equivale determinar L, M y N considerando que están respectivamente alineados con OU, OV y OW, lo que puede hacerse dando una sola coordenada para cada uno de ellos.

Aunque para determinar una referencia proyectiva unidimensional basta con tres puntos cualesquiera (respecto a los cuales cualquier otro determinará una razón doble única), y aún a efectos de asignar coordenadas proyectivas se les pueden atribuir tres valores numéricos cualesquiera, es conveniente por comodidad referirse a puntos como O, U y L con coordenadas como 0, 1 e 'infinito', respectivamente; o sus equivalentes en el espacio, como se muestra en la figura expresando sus coordenadas homogéneas. En estas condiciones es costumbre referise a O como origen, a U, V y W como puntos unitarios y a L, M y N como puntos límite en cada eje de referencia, siendo P el punto unidad.

La proyección como transformación degenerada

Como es sabido, la razón doble se conserva al proyectar; esto significa que al proyectar cuatro puntos como O, U, L y X alineados en un recta x se obtienen otros cuatro también alineados en x' tales que (OULX) = (O'U'L'X'). Por lo tanto la operación de proyectar es en realidad una transformación proyectiva (y perspectiva) especialmente simple. Pero al hacer corresponder un espacio, 3D, con un plano, 2D, tal correspondencia no es biunívoca, por lo que el conocimiento de un punto Q' en el plano de proyección no es suficiente para determinar Q en el espacio.

p> 

Ahora bien, ¿que ocurriría si además de conocer el punto Q' supiésemos, por ejemplo, que Q pertenece al plano OUV? ¿podríamos entonces restituir el punto Q a su posición en el espacio?. Es esta una pregunta clave cuya respuesta no es obvia.

Mientras que la correspondencia entre {OUVWP} y {O'U'V'W'P'} está univocamente definida en 3D, al igual que entre sus equivalentes {OUVWLMN} y {O'U'V'W'L'M'N'}, no ocurre lo mismo cuando la correspondencia resulta degenerada. Aún conociendo la relación de Q con {OUVWP} no es posible determinar Q a partir de Q' y {O'U'V'W'P'} porque la propia relación entre las referencias ha degenerado. Dicho de otro modo, hay infinitas proyectividades (degeneradas) distintas que hacen corresponder una forma como {OUVWP} en 3D con una como {O'U'V'W'P'} en 2D.

No ocurre lo mismo con {O'U'V'W'L'M'N'}, pues, aún siendo una referencia plana, 2D, y por lo tanto degenerada, preserva la información que permite restituir univocamente al espacio la forma {OUVWLMN} conocida [1] y, después, obtener Q a partir de su proyección Q' y cierta información adicional como la sugerida en la pregunta anterior.

La referencia {O'U'V'W'L'M'N'} es, según esto, de mayor calidad, o 'menos degenerada', que la {O'U'V'W'P'}, siendo ésta la razón que nos va a permitir considerar los distintos sistemas de representación como transformaciones degeneradas.

p> 

Qué es una Representación?

Es buen momento para hacerse esta pregunta, y resulta además muy necesaria.

Hemos visto que el concepto de proyección es más restringido que el de transformación e, incluso, que definir una transformación, en particular si ésta es degenerada, requiere ciertas precisiones cuando el objetivo que perseguimos en el de representar, o más precísamente, el de poder restituir al espacio los objetos representados; que es de hecho el principal objetivo de toda representación. Poder 'restituir' significa, no lo olvidemos, poder determinar magnitudes como distancias o ángulos del objeto representado, y en consecuencia áreas, volúmenes, o cualquier otra.

Por un lado, todos los sistemas de representación tradicionales apoyan sus conocimientos 'exclusivamente' en el concepto de proyección, siendo ésta ortogonal, oblícua o central en función del sistema en particular. Sin embargo, hoy en día la representación se hace mayoritariamente con ordenador, realizandose -internamente- cierto tipo de cálculos numéricos que responden más al concepto de transformación que al de proyección.

Aunque una proyección o transformación degenerada por sí sola no es, en general, suficiente para representar un objeto en el espacio, ésta puede vernir acompañada de cierta información, explícita o implícita, que haga posible la restitución y, por lo tanto, permita considerarla como una 'representación' en toda regla. Esta información adicional es habitualmente tan simple como reflejar la pertenencia de un punto a un plano o una recta, o dar a conocer el valor de determinada magnitud angular, reflejar una relación de tangencia, etc.. Así, por ejemplo, una simple proyección ortogonal de un cubo es suficiente para su restitución si, presuponemos -como de hecho hacemos al interpretar una perspectiva axonométrica- que las tres direcciones principales son ortogonales en el espacio, o que un determinado vértice pertenece al mismo plano que los otros tres con los que está configurando una cara, etc.

Aceptando los mismos convencionalismos podemos observar que en la figura a) de la imagen siguiente, por poner otro ejemplo, se percibe una cierta forma prismática; pero no podemos aceptar la misma como una 'representación' correcta en la medida en que no es posible a partir de ella la restitución completa, o la identificación inequívoca de todos sus ángulos. En las figuras b) y c) se ha resuelto el problema -con distintas interpretaciones- de modo que la incertidumbre desaparece al sugerir, con simbolos convencionales en forma de lineas finas, cuales son las tres direcciones ortogonales en el espacio. Es ahora posible la restitución y, por consiguiente, ambas figura b) y c) pueden ser consideradas representaciones correctas de sus respectivos objetos.

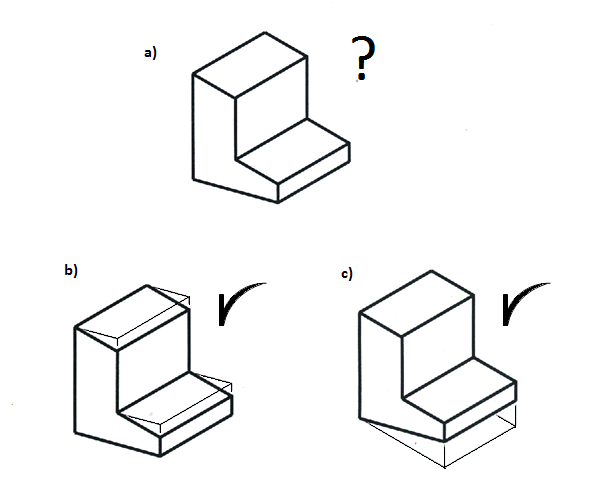
Restitución

Vale, ¿pero entonces que necesito para restituir un objeto (3D) a partir de una representación proyectiva plana (2D)?

Dando por hecho que la información está ahí, necesitamos identificar una referencia completa. Esto es, una referencia 'extendida' de siete puntos {OUVWLMN}, ya que la de cinco {OUVWP} degenera en el plano; o, lo que es lo mismo, tres referencias proyectivas unidimensionales de origen común, O,{OUL}, {OVM}, {OWN}. No es extrictamente necesario que las referencias se correspondan con las coordenadas {0,1,infinito}, pero, será necesario conocer las coordenadas de dos puntos en cada dirección, además de un punto común; pues, conociendo las coordenadas de tres puntos, conocemos las de cualquier otro alineado con ellos. Si sabemos, por ejemplo, que {OUR} se corresponde con coordenadas {0,1,2} podremos obtener el punto límite L tal que (RUOL)=2, o similares.

Basta entonces conocer una referencia y sus dimensiones 'reales' para poder restituir al espacio cualquier punto, recta o plano cuya relación con la referencia se deduzca de la representación.

Sistemas de Representación en el plano.

Los distintos sistemas de representación comúnmente utilizados para representar no son, de este punto de vista, más que casos particulares de una representación general en la que se conoce -o se elige arbitrariamente- un referencia como {OUVWLMN}. Pero, una representación arbitraria, definida por una referencia que se corresponda con su homóloga en un cubo, no tiene poqué ser una proyección 'directa' del espacio sobre el plano de proyección, sino que puede ser obtenida como una proyección de proyección desde éste. En particular, puede ser considerada como una proyección ortogonal de una proyección central del cubo, en la que al elegir la referencia se está definiendo implícitamente -salvo traslaciones u homotecias- del centro y los planos de proyección respecto al cubo. Por ello, si se pretende definir una referencia que responda a la proyección directa del cubo, en alguna de sus distintas formas, conviene estudiar que tienen de particular cada uno de los sistemas. Véase [1]. De este modo, podrá elegirse arbitrariamente parte de la referencia, como {OU..LMN}, y elegir luego el resto {..VW...} de modo que se garantice que de una proyección directa se trata.

Por ejemplo, una 'Perspectiva Aérea' de tres puntos de fuga (correspondientes a las tres direcciones principales) podría obtenerse eligiendo la referencia incompleta {OULMN} y calculando luego V y W de modo {OUVWLMN} corresponda a la proyección central directa de un cubo. Si L, M y N son los puntos límite, o de fuga, por ellos pasan los rayos proyectantes paralelos a las direcciones del cubo a representar. La proyecciones ortogonales del punto de vista y de estos rayos sobre el plano de proyección son H, HL, HN y HM, ortocentro y alturas del triángulo LMN, forzosamente acutángulo.

Un abatimiento del plano CLM alrrededor de LM permite colocarlo en verdadera magnitud y hallar el punto D de fuga de las diagonales del cuadrado OUPV que se trata ahora de representar. Sobre OD y MU se encuentra P de coordenadas (1101) y sobre LP y OM se encuentra V, punto unidad buscado en el eje y. Análogamente puede hallarse W, de coordenadas homogéneas (0011), completando así la referencia con la seguridad de que es proyección directa de un cubo, como se pretendía.

Aunque el término 'Perspectiva Cónica' es usado en ocasiones para referirse a proyecciones centrales (directas) de uno, dos o tres puntos de fuga indistintamente, lo habitual es referirse con él a la de dos puntos de fuga con la tercera dirección vertical. Se obtiene ésta cuando el objeto se sitúa con dos de sus direcciones principales horizontales y la tercera vertical.

En términos de transformaciones esto equivale a elegir una referencia con un punto límite en el infinito, correspondiente al punto de fuga de las lineas verticales, estando los otros dos emplazados en una misma horizontal, denominada linea de horizonte.

Elegidos libremente el origen O y dos puntos unitarios, U y V, puede obtenerse el tercero, W, localizando el punto de fuga D, correspondiente a la dirección diagonal OP, sobre la recta límite LM.

Por 'Perspectiva Lineal' nos referimos a la perspectiva cónica de un solo punto de fuga, esto es, dos puntos límite impropios; lo que equivale a situar dos direcciones principales paralelas al plano de proyección y, como consecuencia, todo lo contenido en planos paralelos al de proyección se proyectará como semejante.

En términos de transformaciones, esto equivale elegir una referencia con L y M impropios y ortogonales, siendo OV = OU.

Si se eligen L, M y N impropios, el resultado es una Axonometría Oblícua.

De particular interés es la Perspectiva Caballera, obtenida cuando además dos direcciones principales son ortogonales y, tratándose de semejanzas, tienen la misma escala. El tercer eje OW puede tener cualquier escala aunque entre 0,5 y 1 es lo más habitual.

Dos casos de este tipo son especialmente utilizados:

a) aquel en el que los dos ejes se situan hozizontal y vertical tomando el eje oblicuo cualquier dirección.

b) aquel en el que los dos ejes en verdadera magnitud se sitúan oblicuos, en relación con el tercero que se situa vertical. Esta representación es muy utilizada en arquitectura, donde mantener el plano horizontal en verdadera magnitud tiene un interés especial.

Para que de una Axonometría Ortogonal se trate es preciso que los puntos unitarios guarden cierta relación con los puntos límite, lo que gráficamente puede garantizarse si, una vez elegidas las direcciones de los ejes (L, M y N) y un OU arbitrario, se calculan convenientemente OV y OW.

Para que una representación proyectiva general sea una perspectiva aérea ha sido preciso que la proyección ortogonal del punto de vista C sobre el plano de proyección coincida con el ortocentro H del triángulo de puntos limite. De modo análogo ahora, para que de una proyección ortogonal se trate es preciso que el origen O de la referencia sea ortocentro de un triángulo como L'M'N', denominado triángulo de las trazas, que representa un triángulo homotético del formado por los L, M y N impropios. O lo que es lo mismo, que tal triángulo tenga sus lados LM, MN y NL ortogonales a OW, OU y OV respectivamente.

Así, la relación entre los puntos unitarios U y V puede establecerse localizando la dirección de las diagonales del cuadrado de lados OU-OV, lo que se ha hecho en la figura abatiendo el triángulo CLM alrrededor de LM hasta situarlo en verdadera magnitud como CoLM. Análogamente puede obtenerse W.

Casos particulares de la axonometría ortogonal son la denominada Perspectiva Dimétrica, en la que las escalas de dos de los ejes resultan iguales, y la Perspectiva Isométrica en la que los tres ángulos son iguales a 120º y las tres escalas son también iguales ex=ey=ez=√(2/3)≈0,816.

------------------

[1] Ver ponencia titulada "Teorema General de la Representación Perspectiva", presentada en el "XI Congreso Internacional de Ingeniería Gráfica" en 1999, a cuya consulta se remite al lector interesado. Baste aquí apreciar que, en efecto, una referencia plana del tipo {OUVWLMN} preserva más información que la de la forma {OUVWP}, pues la cardinalidad del conjunto de referencias degeneradas del primer tipo es ℜ11 (OUVW x 2 coord + LMN x 1 coord = 11) mientras que la del segundo es ℜ10 (OUVWP x 2 coord = 10). En ambos casos la cardinalidad de las referencias en el espacio es R15, (OUVW x 3 coord + LMN x 1 coord = OUVWP x 3 coord = 15).