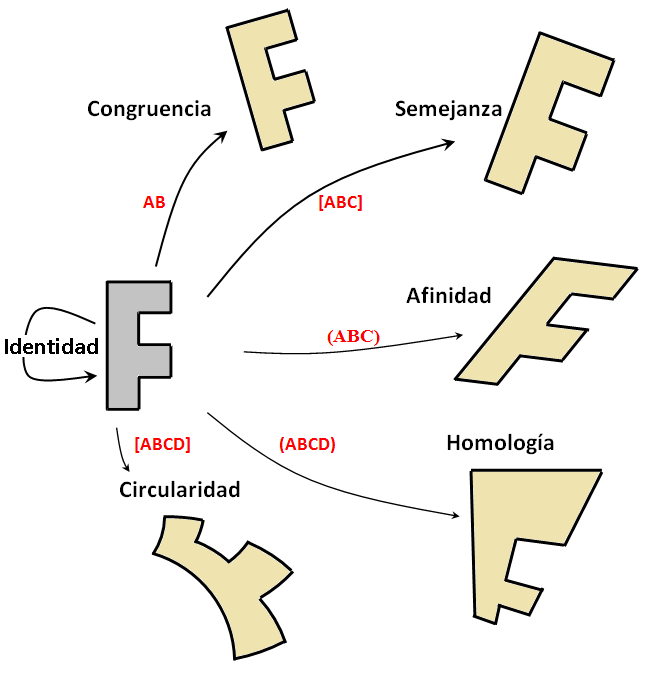
Las transformaciones que se utilizan con más frecuencia en Expresión Gráfica son las transformaciones proyectivas o proyectividades, que podemos clasificar según se muestra en la figura [1].

Cada una de las transformaciones que aparecen se caracteriza por su 'invariante', esto es, por una cierta relación que permanece inalterada en la transformación y que caracteriza plenamente a ésta. Conocer, pues, estas cinco relaciones básicas equivale a conocer las transformaciones y poder sacar de ellas todo lo que pueden ofrecer.

Transformaciones e Invariantes:

A:

Identidad. Por coherencia se da este nombre a la transformación que hace corresponder a cada punto con sí mismo.

AB:

Congruencia o Igualdad. Es aquella transformación que preserva la distancia. Como consecuencia, también se preservan los ángulos, si bien, no necesariamente el sentido, que puede cambiar para toda la transformación. Por conservase la forma y el tamaño de las figuras a estas transformaciones se les denomina también Movimientos, o anti-movimientos, cuando el sentido de los ángulos cambia.

[ABC]:

Semejanza. Se caracteriza por la conservación de la razón simple compleja y, con ella, de los ángulos. Esto es, se conserva la forma aunque varíe el tamaño.

(ABC):

Afinidad. Se caracteriza por la conservación de la razón simple (real) de cada terna de puntos alineados (o de rectas concurrentes). Es ésta una condición necesaria y suficiente para la conservación del paralelismo, que es quizás la propiedad gráfica más notable de esta transformación.[2]

(ABCD):

Homología. Conserva la razón doble (real) tanto de cuaternas de puntos alineados como de cuaternas rectas concurrentes, lo que equivale a significar que conserva la 'linealidad', en el sentido de que las rectas se convierten en rectas. Es pues el caso más general en el que se incluyen todos los anteriores.

[ABCD]:

Circularidad. De modo análogo, se conserva la razón doble compleja. Como propiedad más notable diremos que es ésta una transformación 'conforme', es decir que conserva la forma, entendida ésta en un sentido general; o, para ser más precisos, diremos que conserva 'localmente' los ángulos.

Las transformaciones son uno de los instrumentos más importantes utilizados en Expresión Gráfica. Permiten convertir una figura en otra, que puede ser considerada como una nueva forma de ver la primera y, con ello, a veces transformar un problema en otro más simple; u observar determinadas propiedades desde nuevos puntos de vista, generalizándolas o particularizándolas para obtener nuevas propiedades, extendiendo así su utilidad.

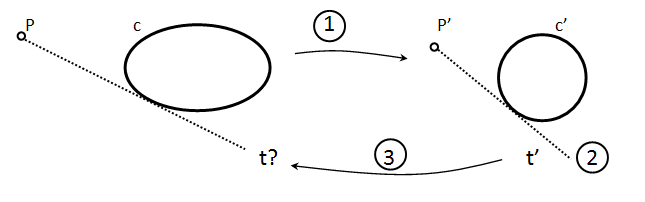
De este modo, por ejemplo, para trazar desde un punto una recta tangente a una elipse, podría elegirse una transformación afín que convirtiese la elipse en circunferencia, de modo que resolver en ésta el problema fuese equivalente, pero más sencillo que problema original.

------------------------