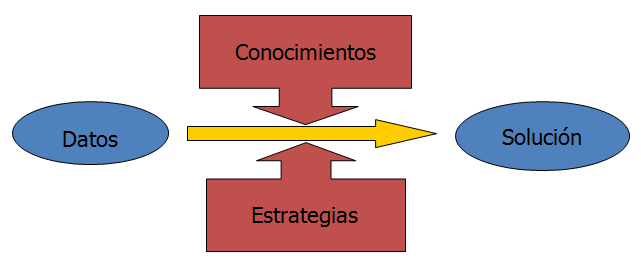
La metodología de resolución de un problema geométrico podría resumirse en el siguiente gráfico:

Esto es, Conocidos ciertos Datos pretendemos obtener otros, a priori desconocidos, que pretenden ser la Solución del problema.
Los datos pueden ser entidades gráficas, relaciones entre éstas o valores numéricos que determinan alguna de sus propiedades.
Muchas veces los datos están expresados directamente en un enunciado, en otras, como ocurre cuando uno mismo se plantea un problema, el propio enunciado es parte del problema, y definirlo con precisión, esto es 'tener claro cual es el objetivo', es el primer gran paso en la búsqueda de la solución.
Resolver un problema gráfico es encontrar un camino, o 'algoritmo', que nos permita encontrar la solución buscada a partir de los datos conocidos. Y para ello es preciso, claro está, tener cierto bagage de conocimientos, pero también -y con frecuencia no se da a esto la importancia que merece- disponer de las habilidades o estrategias necesarias.
Si de alguna manera quisiésemos clasificar los Conocimientos más destacados en la resolución de los ejercicios, cabría mencionar con cierto énfasis los relativos a:
-Figuras geométricas y su propiedades.
-Relaciones: AB, <ABC, (ABC), [ABC], (ABCD), [ABCD]
-Lugares geométricos o envolventes, descritos por un punto, linea o superficie que satisface una determinada propiedad.
-Potencia y conceptos derivados.
-Cónicas y otras curvas técnicas
-Transformaciones geométricas (proyectivas y perspectivas), que permiten muchas veces transformar un ejercicio en otro, etc.
-Sistemas de Representación.
Al hablar de Estrategias para la resolución de un problema, podrían también significarse distintos métodos, tácticas o 'trucos':
- Métodos sintéticos o geométricos ( 'lugares geométricos', 'reducción', 'dilataciones', 'problema contrario', 'falsa posición', etc.)
- Métodos algebraicos o analíticos ('directo', 'paramétrico', 'vectorial', complejo',..).
- Y un sinfín de tácticas y formas de... !hacerse preguntas!